"integracion por partes"

mi aprendizaje:

me di la tarea de buscar informacion y ejercicios en youtube, algunos son faciles pero ahi otros que si se ven un poco complicados. estare revisando mas videos para poder complementar bien la informacion ya que no tengo del todo despejado el tema.

informacion complementaria:

A diferencia de las derivadas, no existe una fórmula para poder integrar cualquier producto de funciones. Lo más cercano que tenemos a una regla para integrar producto de funciones es la integración por partes. Curiosamente, se basa en la fórmula para derivar un producto de funciones.

sin embargo, la integración por partes transforma una integral de un producto en otra integral. Esta fórmula no funciona para integrar todos los productos de funciones

La fórmula de la integración por partes es

$\text{[math]}$

Observemos que tenemos que derivar $\text{[math]}$ e integrar $\text{[math]}$ , por lo que será conveniente que la integral de $\text{[math]}$ sea sencilla.

En general, las funciones polinómicas, logarítmicas y arcotangente se eligen como $\text{[math]}$ . Mientras que las funciones exponenciales, seno y coseno se eligen como $\text{[math]}$ .

ejemplo:

Tenemos el producto $x \cdot e^{x}$ .

Observad que la exponencial no cambia al derivar ni al integrar, así que no importa si le asignamos $u$ ó $d v$ .

No ocurre lo mismo con $x$ :

Al derivar se reduce su exponente en 1 y pasa a ser una constante.
Al integrar aumenta su exponente en 1.

Por tanto, la elección más apropiada es $u = x$ y $d u = d x$ .

Derivamos $u$ para calcular $d u$ :

Cálculo de primitivas, integración por partes: integrales resueltas paso a paso y explicadas. Método de integración por partes, consejos y ejemplos de aplicación. Integrales cíclicas, aplicación sucesiva del método... Bachillerato. Análisis de una variable.

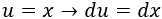
Integramos $d v$ para calcular $v$ :

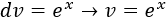
Aplicamos la fórmula de integración por partes:

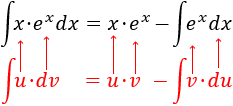
Finalmente, resolvemos la nueva integral (la de la exponencial) y añadimos la constante de integración $C \in R$ :

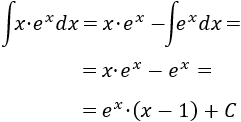
Nota: como ya hemos dicho, es importante escoger $x = u$ para reducir el grado del monomio al derivar. Si por el contrario hubiésemos escogido $x = d v$ , entonces $v = \frac{x^{2}}{2}$ , aumentando el grado (de 1 a 2) y complicando más la integral, pues el factor de la exponencial se mantiene igual y nos aparece la integral